Vamos começar o estudo da Integral de funções com fracções, primeiramente vamos aprender funções bem simples de integral (funções que são integradas de forma imediata).
Como integral uma função do tipo;
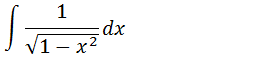
Para integrar essa função devemos nos recordar da derivada da função inversa da função seno (a função arcsen(x))
A derivada da função arcsen(x) é a função 1/√(1-x2)
O que quer dizer que a integral da função 1/√(1-x2) é a função arcsen(x) e podemos escrever;
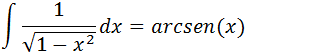
Para generalizar a nossa solução vamos colocar a nossa constante
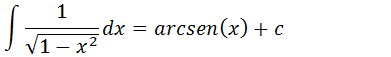
Usando as formulas aprendidas anteriormente
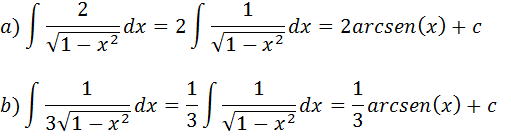
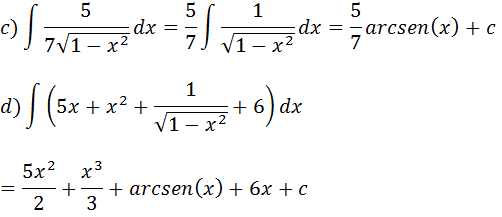
Formula generalizada da integral que resultam em arcseno
Dentro da raiz nem sempre será 1-x2 , as vezes podemos ter casos onde dentro da raiz no denominador tenhamos 2-x2 , 3-x2 , 6-x2 ,,,,então convém achamos uma formula para integral esses casos onde dentro da raiz não vem 1-x2
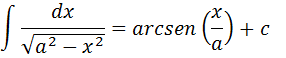
Demonstração da formula generalizada da integral que resultam em arcseno
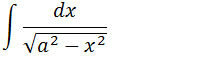
Para fazermos a demonstração vamos transformar essa integral em uma integral ja conhecida para isso vamos fazer articulações matemáticas de modo que dentro da raiz tenhamos somente uma expressão 1-u2 para isso primeiramente vamos tirar o a para fará da raiz.
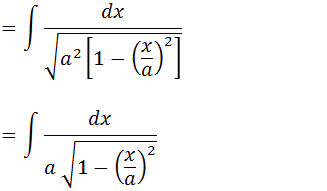
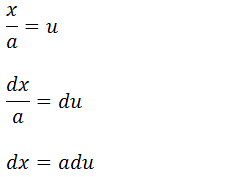
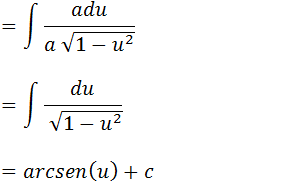
Vamos substituir u por x/a e assim temos demostra
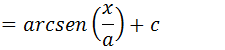
Exercícios de calculo de integrais que resultam em funções trigonométricas inversas arcseno
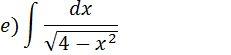
Vamos transformar 4 em 22 e aplicar a nossa forma vista acima
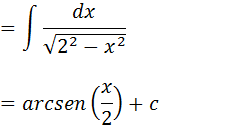
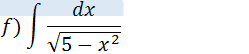
vamos colocar raiz no cinco e elevar ao quadrado;
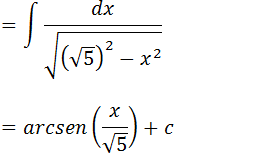
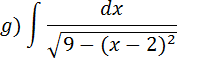
Vamos transformar 9 em 32
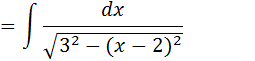
Vamos usar o método de substituição….
Seja ; x-2=u
dx=du
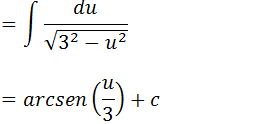
Vamos substituir o u por x-2 e assim temos a nossa integral calculado.
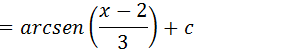
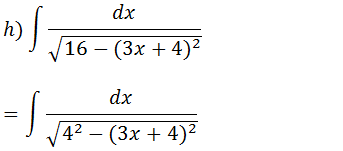
Seja ; 3x+4=u
3dx=du
dx=du/3
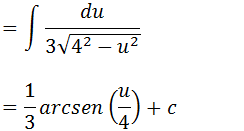
Substituindo “u” por “3x+4” temos;
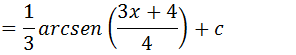
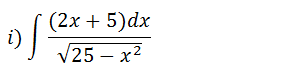
Primeiramente vamos separar a nossa integral em duas integral
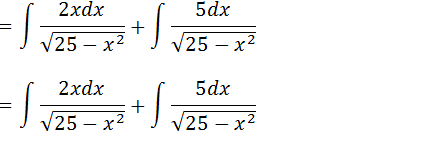
Vamos calcular cada integral separadamente depois somar as duas integrais
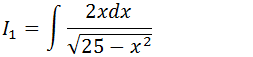
25-x2=t
2xdx=dt
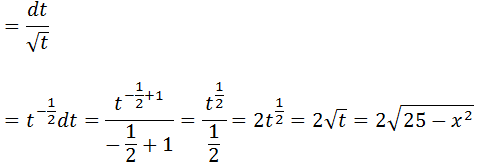
Agora vamos calcular a segunda integral
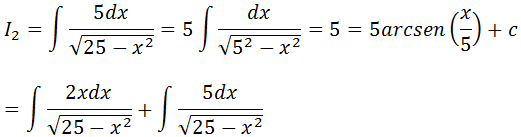
I=I1+I2
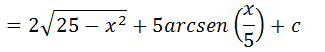
Aulas relacionadas
- Calculo integral
- Derivada de arcseno
- Integral de funções exponencial
- Derivada de funções trigonométricas
- Limites trigonométricos
Calculadora Casio fx-991 Plus
Maquina de calcular Casio fx-991 Plus Temos disponível calculadora cientifica Casio fx-991 Plus, est…
Livro de calculo integral
Livro de calculo Integral Caso você queira aprender calculo integral recomendamos a você adquirir o …
Apostila de Cálculos de limites (Ebook de calculo I)
Apostila de cálculo de limite Você sabia que tem um Ebook de cálculo de limites que pode ajudar você…
Integral de fracções fraccionarias
Integral de funções do tipo Para integramos essa função vamos transformar a expressão que esta na ra…
Integral de funções com fracções
Integral de funções que resultam em arctag(x) Essa é uma integral imediata, bastando apenas nos reco…
Integral de funções com fracções ( com raiz no denominador)
Integral de fracções com raiz no denominador Primeiro tipo Para integramos essa função vamos transfo…
Integral de funções que resultam em arcseno
Vamos começar o estudo da Integral de funções com fracções, primeiramente vamos aprender funções bem…
Integrais por partes (calculo integral usando o método de integrais por partes)
Integrais por partes A técnica de Integral por partes é uma técnica usada para simplificar a resoluç…
Integral usando o método de substituição
Usar uma substituição no cálculo integral torna-se indispensável para resolver diversos exercícios d…









