Integral de funções com fracções ( com raiz no denominador)

Integral de fracções com raiz no denominador Primeiro tipo

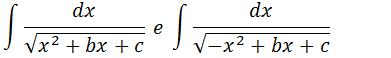
Para integramos essa função vamos transformar a expressão que esta na raiz numa expressão do tipo

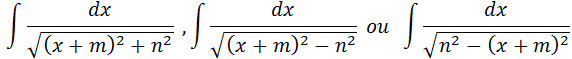
Relembrando as formulas de integrais que fracções com raiz no denominador;

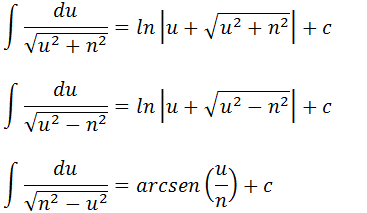
Onde para as nossas integrais o “u” vale “x+m” então as soluções das nossas integrai serão;

Resolução de exercícios Integral de funções com fracções com raiz no denominador

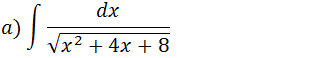
Vamos transformar a expressão que esta na raiz numa expressão do tipo (x+m)²+n²

x²+4x+8=x²+2•2x+8= x²+2•2x+2²-2²+8=(x+2)²+4

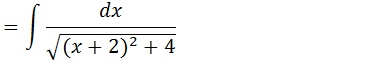
Transformaremos 4 em 2 ao quadrado e depois iremos usar a nossa forma de integral de uma fracção dentro da raiz e assim temos o resultado da nossa integral.

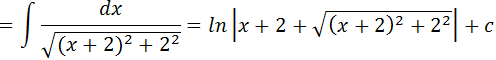
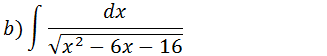
sabemos que x²-6x-16=x²-2•3x-16= x²-2•3x+3²-3²-16=(x-3)²-25 substituindo x²-6x-16 por (x-3)²-5² na nossa integral temos :

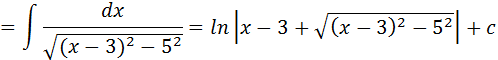
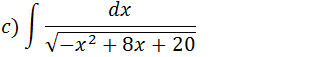
Recorrendo aos mesmos procedimento que fizemos nos exercícios acima

-x²+8x+20=-(x²-8x-20)= -(x²-2•4x+4²-4²-20)=-((x+4)²-36)=-( x+4)²+6²

-( x+4)²+6² podemos escrever como 6²-( x+4)² e nos recordamos das integrais que resultam em arcseno

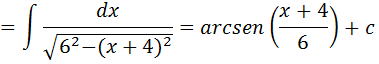
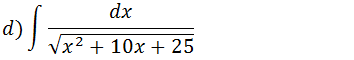
Iremos escrever a expressão que esta dentro da raiz como x²+10x+25=x²+2•10x+5²=(x+5)²

Simplificaremos o ao quadrado com a raiz e assim teremos integral de 1 sobre x+5 e essa integral resultam em ln |x+5|.

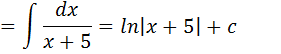
Integral de fracções com raiz no denominador segundo tipo

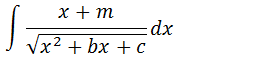
Nesse tipo de integral precisamos de ter a derivada da expressão que esta dentro da raiz no numerador adicionado a uma constante depois separa a integral em duas integrais e por fim resolver cada uma das integrais.

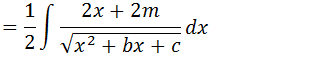
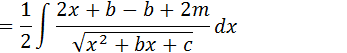
Separamos a nossa integral em duas integrais

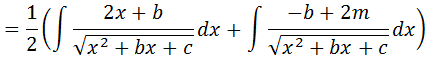
Tirando as contastes que estão dentro da integral para fora da integral temos;

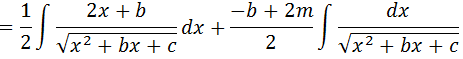
Devemos por fim calcular I₁ e I₂ e assim temos a solução da nossa integral

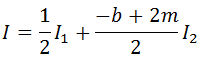
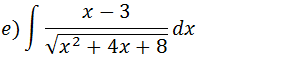
Vamos seguir os passos que aprendemos anteriormente , Vamos multiplicar o numerador por 2 e multiplicar a nossa integral por (1/2) para tirar o dois que nos multiplicamos no numerador

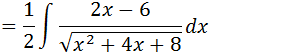
Como queremos ter a derivada da expressão que esta na raiz no numerador vamos adicionar 4 e subtrair 4

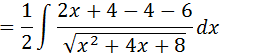
Vamos somar -4 e -6 que resulta em -10

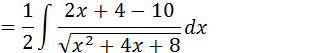
Separando a nossa integral em duas integrais temos;

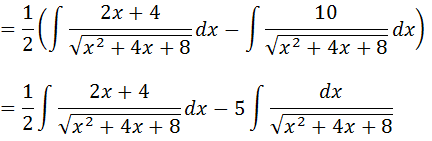
Vamos calcular cada uma das nossas integrais

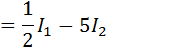
Agora vamos calcular a primeira integral, como a derivada da expressão que esta na raiz esta no numerador vamos usar o método de substituição

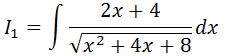
x²+4x+8=u

(2x+4)dx=du

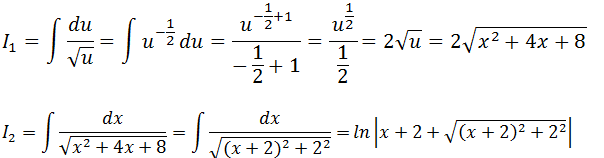
Vamos agora para integral principal

Substituindo I₁ e I₂ pelas espressoes equivalentes temos

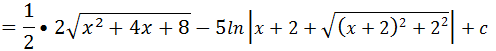
Simplificaremos o 1/2 e 2 e escreveremos (x+2)²+2² como sendo x²+4x+8

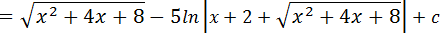
A solução do nosso exercício é :

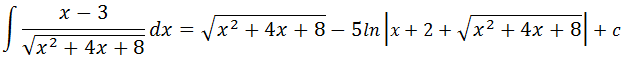
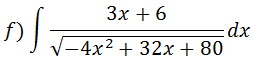
Para resolver essa integral primeiro vamos tirar o 4 para fora da raiz

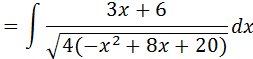
Evidenciando o 3 no numerador e tirando o 4 para fora de raiz temos;

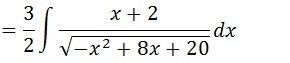
Vamos multiplicar o numerador por -2 e multiplicar a nossa integral por (-1/2) para que seja uma expressão equivalente.

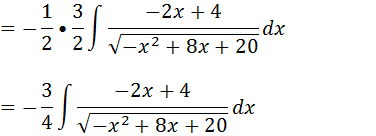
Para que a derivada da expressão que esta dentro raiz esteja no numerador no numerador temos que ter -2x+8 ja temos o -2x falta o 8 então vamos adicionar 8 e tirar 8 (+8-8)

Somando -8 e 4 temos -4;

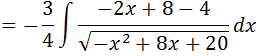
Aplicando a propriedade da integral da soma iremos separar a nossa integral em duas integrais

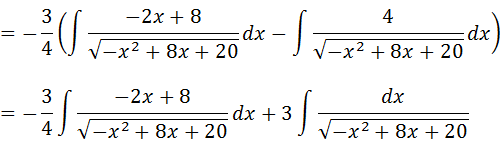
Vamos calcular separadamente dada uma das integrais

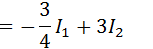
Calcularemos a primeira integral (I₁) usando o método de substituição

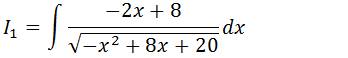
-x²+8x+20=u

(-2x+8)dx=du

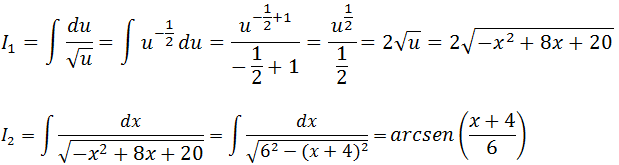
Iremos agora substituir a expressão de I₁ e I₂ na nossa integral principal

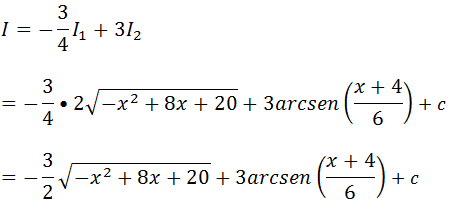
Já temos a solução do nosso exercício que é :

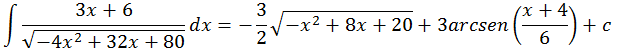
Aulas relacionadas

• Calculo integral
• Derivada de arcseno
• Integral de funções que resulta em uma função logaritmo
• Integral de funções exponencial
• Integral de método substituição
• Limites trigonométricos