Como integral uma função do tipo?

Como forma de introdução e para facilitar a nossa compressão nessa aula primeiro vamos fazer uma breve revisão sobre a formula de integrais de função polinomial.
Já aprendemos a integral usando a formula ;
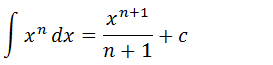
Com essa fórmula podemos integral funções do tipo;


Agora se n=-1 usando a mesma formula temos;

Nesse caso de n=-1 a nossa fórmula não se aplica
A fórmula para integral uma função do tipo ∫ xn dx tem uma limitação quando o nosso n for -1, pois se o nosso n for -1 no denominador teremos -1+1=0 e conforme sabemos não existes divisão por zero.
Então como Integral uma expropriação do tipo ∫ xn dx quando n for igual a -1
Para integrar esse tipo de função devemos nos recordar da derivada de funções logaritmicas, onde vimos que a derivada de y=ln(x) é y’=1/x , o que quer dizer que;
∫ 1/x dx=ln(x)
Então essa é a fórmula que usaremos para integrar esse tipo de funções
Fórmula de Integral de uma funções que resultam em função logaritmicas
Conforme a demonstração acima a integral da função 1/x tem como resulto uma função logarítmica que é ;

Resolução de exercícios sobre Integral de uma funções que resultam em função logaritmicas

Iremos primeiro tirar o quatro para fora da integral fazendo isso dentro da integral ficamos apenas 1/x e a integral de 1/x vale ln|x|.


Vamos tirar o 3 para fora da integral e depois integral a expressão que fica dentro da integral.


como a derivada de do que esta no denominador é exactamente o que esta no numerar essa integral resulta em “ln” do que esta no denominador.


A derivada de -3x+2 é -3 então vamos colocar -3 no numerador para que a derivada de -3x+2 esteja no numerador e assim a integral resulte em “ln”

Mais exercício sobre calculo integral Integral de uma funções que resulta em função logaritmo

Como nesse caso é possível termos a derivada do denominador no numerador apenas multiplicando por constante. vamos arranjar uma maneira de dermos a derivada de x2+1 no numerador para que a integral resulte em “ln”. A derivada de x2+1 é 2x no numerador já temos x o que falta é apenas multiplicar o x por 2 vamos fazer isso(multiplicar o x por dois e tirar esse dois que colocamos multiplicando por 1/2).


É notório que a derivada de ex+1 é ex ,logo essa integral resulta em ln|ex+1|


A derivada de x2+3x-5 é exactamente o que esta no numerador ,com isso essa integral resulta em ln|x2+3x-5|.


Notamos claramente que a derivada de 2x7+5x3 -8x+1 é 14x6 +15x2-8 , logo a essa integral é uma integral do tipo ∫ du/u onde o nosso u é 2x7+5x3 -8x+1 e o nosso du é (14x6 +15x2-8)du, como ∫ du/u=ln|u| a nossa integral é igual a ln|2x7+5x3 -8x+1|

Veja Essa aula em video
Veja outras aulas sobre logoritmos
Aulas relacionadas
- Calculo de Limite
- Derivada de funções logarítmicas
- Equações logarítmicas
- Inequações logarítmicas
- Funções logarítmicas
Calculadora Casio fx-991 Plus
Maquina de calcular Casio fx-991 Plus Temos disponível calculadora cientifica Casio fx-991 Plus, est…
Livro de calculo integral
Livro de calculo Integral Caso você queira aprender calculo integral recomendamos a você adquirir o …
Apostila de Cálculos de limites (Ebook de calculo I)
Apostila de cálculo de limite Você sabia que tem um Ebook de cálculo de limites que pode ajudar você…
Integral de fracções fraccionarias
Integral de funções do tipo Para integramos essa função vamos transformar a expressão que esta na ra…
Integral de funções com fracções
Integral de funções que resultam em arctag(x) Essa é uma integral imediata, bastando apenas nos reco…
Integral de funções com fracções ( com raiz no denominador)
Integral de fracções com raiz no denominador Primeiro tipo Para integramos essa função vamos transfo…
Derivada de uma função usando definição
Definição de derivadas Chamamos de derivada da função f(x) no ponto qualquer a inclinação …
Derivada de uma função
Depois de termos aprendendo o conceito de derivada agora é a hora de aprendemos a cal…
Derivada de funções implícitas
Antes de aprendermos a derivar uma função implícita é necessário saber o que é uma fu…
Derivada de funções paramétricas
Derivada de funções paramétricas Seja y=f(t) e x=g(t) nesse caso podemos afirmar que…
Cálculo de limite usando L’Hospital (Cálculo de limite usando derivadas)
Regra L’Hospital para o calculo de limite A regra de L’Hospital consiste em utilizar o conhecimento …
Cálculo de derivada usando logaritmização
Calcular derivada usando logaritmização ajuda-nos a resolver derivadas que parecem difícil de c…
Limite notável (limite exponencial)
O Limite notável é base para a resolução de diversos limites exponencial épraticamente impossível re…
Limite exponencial (limite de Euler)
Limite exponencial são conhecido vulgarmente como limite de Euler, a indeterminação nos li…
Limites indeterminações do tipo infinito sobre infinito
Limites contendo indeterminações do tipo infinito sobre infinito são limites&nbs…
Limites indeterminações do tipo infinito menos infinito
Agora que já aprendemos as propriedades dos limites , como resolver exercícios de lim…
Limites de funções de variável real
Representação de limite Seja da uma função f(x) e nós desejamos saber qual é o limite da f…
Propriedades usadas no cálculo de limites
As propriedades usadas do cálculo de limites na maioria das vezes são empregues de forma …














