Vamos começar o estudo da Integral de funções com fracções, primeiramente vamos aprender funções bem simples de integral (funções que são integradas de forma imediata).
Como integral uma função do tipo;
Para integrar essa função devemos nos recordar da derivada da função inversa da função seno (a função arcsen(x))
A derivada da função arcsen(x) é a função 1/√(1-x2)
O que quer dizer que a integral da função 1/√(1-x2) é a função arcsen(x) e podemos escrever;
Para generalizar a nossa solução vamos colocar a nossa constante
Usando as formulas aprendidas anteriormente
Formula generalizada da integral que resultam em arcseno
Dentro da raiz nem sempre será 1-x2 , as vezes podemos ter casos onde dentro da raiz no denominador tenhamos 2-x2 , 3-x2 , 6-x2 ,,,,então convém achamos uma formula para integral esses casos onde dentro da raiz não vem 1-x2
Demonstração da formula generalizada da integral que resultam em arcseno
Para fazermos a demonstração vamos transformar essa integral em uma integral ja conhecida para isso vamos fazer articulações matemáticas de modo que dentro da raiz tenhamos somente uma expressão 1-u2 para isso primeiramente vamos tirar o a para fará da raiz.
Vamos substituir u por x/a e assim temos demostra
Exercícios de calculo de integrais que resultam em funções trigonométricas inversas arcseno
Vamos transformar 4 em 22 e aplicar a nossa forma vista acima
vamos colocar raiz no cinco e elevar ao quadrado;
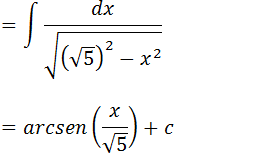
Vamos transformar 9 em 32
Vamos usar o método de substituição….
Seja ; x-2=u
dx=du
Vamos substituir o u por x-2 e assim temos a nossa integral calculado.
Seja ; 3x+4=u
3dx=du
dx=du/3
Substituindo “u” por “3x+4” temos;
Primeiramente vamos separar a nossa integral em duas integral
Vamos calcular cada integral separadamente depois somar as duas integrais
25-x2=t
2xdx=dt
Agora vamos calcular a segunda integral
I=I1+I2
Aulas relacionadas
- Calculo integral
- Derivada de arcseno
- Integral de funções exponencial
- Derivada de funções trigonométricas
- Limites trigonométricos
Teoria do Comportamento do Consumidor
O que faz com que determinado consumidor com uma renda limitada decida que bens ou serviços adquirir…
Elasticidade da Oferta e da Demanda
Tanto a oferta, assim como a Demanda por qualquer bem são influenciados pela variação de diversos fa…
Equilíbrio de Mercado: Preço e Quantidade de Equilíbrio
Conforme dito na matéria sobre os Fundamentos da Oferta e Demanda, a teoria da oferta e demanda é a …
Factores que influenciam a curva da Demanda
Já foi explicado na matéria sobre Os fundamentos da oferta e demanda que a Curva da Demand…
Factores que influenciam a curva da Oferta
Conforme dito no artigo sobre os Fundamentos da Oferta e da Demanda, a curva da oferta informa-…
Os Fundamentos da Oferta e da Demanda
Com toda a certeza, o modelo da oferta e demanda é o instrumento-chave da microeconomia ( pode ver d…
Resolução de (Teste I) de Calculo I UNIFEI
1) Calcule caso exista. Se não existir explique o por quê:Primeiro vamos Substituir onde vem x pela …