Movimento harmónico simples e equações de Thompson para pêndulos

Movimento harmónico simples (MHS)

Movimento harmónico simples (MHS) são movimentos mecânicos em que os corpos repetem periodicamente o seu movimento.

Seja um corpo realizado um movimento de vai e vem do ponto P para o poço Q.

O ponto O é chamado de ponto de equilíbrio

Período de um Movimento harmónico simples

Chamaremos de período o tempo que ele vai levar para sai de ponto Para ir ao ponto Q e regressar ao ponto P

Amplitude

Chamaremos de amplitude o afastamento Máximo em relação a posição de equilíbrio.

Frequência cíclica

Frequência cíclica é rapidez com que o ângulo das oscilações varia ao longo do tempo.

Equações do Movimento harmónico simples (MHS)

No movimento harmónico simples veremos três equações que são a equação da elongação, equação da velocidade e a equação da aceleração. Primeiramente iremos determinar a equação da elongação e por seguinte iremos determinar a equação da velocidade e da aceleração, equação da velocidade é obtida derivando a equação da elongação, e a equação da aceleração é obtida derivando a equação da velocidade.

Equação da elongação em função do tempo

A elongação y pode facilmente ser determinada a par de relações trigonométricas

y=Asenɸ

y=A•sen(ωt+ɸ˳)

Equação da elongação em função do tempo

Gráfico da elongação em função do tempo

Onde;

A→ Elongação máxima

-A→ Elongação mínima

T→ Período

 Nota; A amplitude representa a elongação máxima

Equação da velocidade em função do tempo no movimento harmónico simples

A velocidade da partícula representa a taxa de variação temporal da elongação em função do tempo, portanto para encontrar a velocidade iremos usar o conceito de que a velocidade é a derivada da elongação.

v=A•ω•cos(ωt+ɸ˳)

Equação da velocidade em função do tempo

Gráfico da velocidade em função do tempo

Onde;

A•ω→ Velocidade máxima

-A•ω→ Velocidade mínima

T→ Período

Nota; produto da amplitude com a frequência cíclica representa a velocidade máxima

Equação da aceleração em função do tempo no movimento harmónico simples

A aceleração da partícula representa a taxa de variação temporal da velocidade em função do tempo, portanto para encontrar a velocidade iremos usar o conceito de que a velocidade é a derivada da elongação.

a=-A•ω²•sen(ωt+ɸ˳)

Equação da aceleração em função do tempo

 Gráfico da aceleração em função do tempo

Onde;

A•ω²→ Aceleração máxima

– A•ω²→ Aceleração mínima

T→ Período

Nota;O produto da amplitude com o quadrado da frequência cíclica representa a aceleração máxima

Exercícios de aplicação Movimento harmónico simples

1. Um corpo Material realiza MHS de acordo com o gráfico , calcule;

a) o valor do período

b) a amplitude

c) a equação da elongação

d) o valor da aceleração no instante t= 6π s

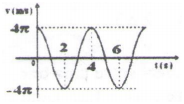
Resolução

a) Periodo  é o tempo que que leva para fazer uma volta completa

T=4s

b)A equação da velocidade para O Movimento Harmónico simples (MHS) conforme vimos acima  é da do por v=A•w•cos(wt) o valor máximo é Aw e o valor mínimo é –Aw

No gráfico o valor máximo é 4π Então;

 Aw=4π

c) A equação da elongação é y=A•sen(ωt+ɸ˳)

d) Para encontrar o valor da aceleração no instante t= 6 s devemos primeiro encontrar a equação da aceleração

Podemos encontrar a equação da aceleração derivando duas vezes a equação da elongação

Agora tendo a equação da aceleração é só substituir t=6 s

Equação de Thompson pêndulo simples

Período de um pêndulo simples

Sobre o corpo actua o peso e o mesmo esta sujeita a uma aceleração centrípeta então a forca resultante será uma resultante centrípeta.

P=Fc

Equação de Thompson pêndulo simples

Equação de Thompson para pêndulo elástico

Período de um pêndulo elástico

No pêndulo elástico o quadrado da frequência cíclica é igual a razão ente a constante elástica da mola e a massa do corpo.

Equação de Thompson para um pêndulo elástico

Exercício de aplicação

1.Um corpo de massa 5 kg, preso a extremidade de uma mola oscila com período de 0,2s determine a constante elástica da mola?

Resolução

Dados

m=5kg

T=0,2 s

R; A constante elástica da mola é de 5000N/m

---

Mais aulas de Física