O que é estudo completo de uma função ?
Fazer o estudo complete de uma função significa indicar;
1.O domínio função
2.O contra domínio função
3.Os zeros da função
4. A ordenada na origem
5.As coordenadas dos vértices
6.O eixo de simetria
7.A variação do sinal
8.Estudar a monotonia
9.Indicar a expressão analítica
1.Domino de uma função do segundo grão
O domínio de uma função do segundo grão é sempre x ∈ IR
2.O contra domínio função
O contra domínio de uma função são todos os valores de y , que a função assume. O contra domínio de uma função do segundo grão é:
*y ∈ [yv ,+∞[ se o valor de “a” positivo;
*y ∈ ] -∞, yv] se o valor de “a” negativo.
3.OS Zeros da função
Os zeros da função são os valores de x na qual a função intercepta o eixo das abcissas, onde para uma função quadrática são; x=x1 e x=x2
4. A ordenada na origem
A ordenada na origem é o valor de y para x=0 ou seja é o valor de y onde a função intercepta o eixo das ordenadas. Para uma função quadrática a ordenada na origem corresponde ao valor do parâmetro “c” (y=c).
5.As coordenadas dos vértices
As coordenadas dos vértices são o xv e o yv. (xv,yv)
6.O eixo de simetria
O eixo de simetria é onde a função se divide em duas partes iguais para uma função do segundo grão é x=xv ( a função quadrática sempre se tive em duas partes iguais no xv)
7.A variação do sinal
Estudar a variação de sinal significa indicar onde a função é positiva e onde a função é negativa.
8.Estudar a monotonia
Fazer o estudo da monotonia de uma função é indicar o intervalo onde a função é crescente e onde a função é decrescente.
| a>0 | ] – ∞ ,xv[ é decrescente | ] xv , +∞[ é crescente |
| a<0 | ] – ∞ ,xv[ é crescente | ] xv , +∞[ é decrescente |
9.Indicar a expressão analítica
A principio expressão analítica é uma equação matemática y=f(x) capaz de descrever o gráfico. a expressão analítica de uma função quadrática é f(x)=ax2+bx+c.
Expressão analítica de uma função quadrática
As formulas para encontrar a expressão a analítica de uma função do segundo grão são as seguintes:
y=a(x-x1)(x-x2) ou
y=a(x-xv)2+yv
*A primeira formula só podemos usar quando a função tiver o zeros da função (x1 e x2) e este estiverem explícitos no gráfico, note que nem toda função quadrática tem zeros.
*A segunda formula usamos quando os vértices estão explícitos no gráfico como todos gráficos das função quadráticas tem vértices essa forma não tem muita limitação na sua aplicação.
Como achar expressão analítica de uma função quadrática?
Para encontrar a expressão analítica de uma função quadrática basta usar uma das formulas y=a(x-x1)(x-x2) ou y=a(x-xv)2+yv
Passos para achar a expressão analítica de uma função do segundo grão usado os zeros da função
1.Conhecer a formula y=a(x-x1)(x-x2)
2. A partir do gráfico indicar x1 e x2 e escolher um ponto no gráficos com valores de (x ,y)
3. Substituir os valores de y, x, x1 e x2 na equação e achar o valor de “a”
4. Depois de encontrar o valor de “a”, substituir na equação y=a(x-x1)(x-x2) , a, x1, x2 pelos respectivos valores e assim achamos a achamos a expressão analítica.
Passos para achar a expressão analítica de uma função do segundo grão usado os vértices ( xv e yv.)
1.Conhecer a formula y=a(x-xv)2+yv
2. A partir do gráfico indicar os vértices xv e yv e escolher um ponto no gráficos com valores de (x ,y)
3. Substituir os valores de y, x, xv e yv na equação y=a(x-xv)2+yv e achar o valor de “a”
4. Depois de encontrar o valor de “a”, substituir na equação y=a(x-xv)2+yv , a, xv, yv pelos respectivos valores e assim achamos a achamos a expressão analítica.
Exercícios resolvidos para fazer o estudo completo de uma equação quadrática
1.Seja dado o gráfico a seguir de uma função quadrática
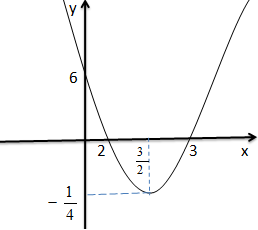
A partir do gráfico indique;
a) O domínio
b)A ordenada na origem
c)Os zeros da função
d)Faca o estudo do sinal
e)A monotonia
f)Qual é a expressão analítica do gráfico
Resolução
a) Df; x ∈ é IR ( o domínio de uma função do segundo grão é sempre IR)
b)A ordenada na origem é y=6
c)Os zeros da função são x=2 e x=3
d)Estudo do sinal
| ] – ∞ ,2[ | ]2, 3[ | ]3, +∞[ | |
| f(x) | + | – | + |
Outra alternativa de fazer o estudo da variação de sinal é ;
] – ∞ ,2[U]3, +∞[ é positivo
]2, 3[é Negativo
e)Monotonia da função
| ] – ∞ , 3/2[ | ] 3/2 ,+∞[ | |
| f(x) | Decrescente | Crescente |
f)Expressão analítica do gráfico
A partir do gráfico podemos notar que quanto x=0, y=6 e os zeros são x1=2 e x2=3
Para achar a expressão analítica vamos usar a fórmula”y=a(x-x1)(x-x2)” onde primeiramente iremos fazer a subistituição dos valores de x,y,x1 e x2 e obter o valor de “a”.
y=a(x-x1)(x-x2)
6=a(0-2)(0-3)
6=a(-2)(-3)
6=6ª
6a=6
a=6/6
a=1
Agora com o valor de “a” já calculado vamos achar a expressão analítica substituindo os valores de a, x1, x2 na equação y=a(x-x1)(x-x2).
y=a(x-x1)(x-x2)
y=1(x-2)(x-3)
y=(x-2)(x-3)
y=x2-3x-2x+6
y=x2-5x+6
Portanto a expressão analítica da função representado no gráfico é y=x2-5x+6
2.Faca o estudo completo da função indicado;

a) O domínio e o contra domínio
b)A ordenada na origem
c)Os zeros da função
d)A variação do sinal
e) Estude a monotonia
f)Qual é a expressão analítica do gráfico
Resolução
a) Domínio e o contra domínio
Df; x ∈ IR
D’f : y ∈ ]1; +∞[
b)A ordenada na origem é y=4
c)Os zeros da função
a função não tem zeros
d)A variação do sinal
A função é sempre positiva
e) Estudo da monotonia
| ] – ∞ , 1[ | ] 1 ,+∞[ | |
| f(x) | Decrescente | Crescente |
f)Determinação da expressão analítica do gráfico
Como a função não tem zeros para achar a expressão analítica “só” podemos recorrer a forma “y=a(x-xv)2+yv“ para achar a expressão analítica.
Os vértices (observando no gráfico) são xv=1 e yv=1 e quando x=0, y=4
Vamos substituir esses valores na formula da expressão analítica para achar o valor de “a”.
y=a(x-xv)2+yv
4=a(0-1)2+1
4=a(-1)2+1
4=a•1+1
a=4-1
a=3
Tendo o valor de “a” , e os vértices, iremos na formula y=a(x-xv)2+yv substituindo “a” pelo respectivo valor, xv, pelo respectivo valor yv pelos respectivo valor e assim temos a expressão analítica
y=a(x-xv)2+yv
y=3(x-1)2+1
y=3(x2-2x+1)+1
y=3x2-6x+3+1
y=3x2-6x+4
Desta forma podemos dizer que a expressão analítica da função é y=3x2-6x+4
Exercícios sobre estudo de função (função quadrática) para praticar
Seja dados os gráficos;


Para cada um dos gráficos determine;
1.O domínio
2.O contra domínio
3.Os zeros
4. A ordenada na origem
5.As coordenadas dos vértices
6.O eixo de simetria
7.A variação do sinal
8. A monotonia
9.Determine a expressão analítica
Vejas mais aulas de Matemática
Resolução do exame de admissão ao ifp 2023
Acompanhe a resolução do exame de matemática admissão ao Instituto de formação de professores (IFP) …
Manual de preparação para exames de admissão de matemática ao IFP ano lectivo de 2024
Temos manual de preparação para exames de admissão de matemática ao IFP para o ano lectivo de 2024. …
Generalidades em equações paramétricas
Generalidades em equações paramétricas Podemos ter casos complexos em que o parâmetro se transforme …
Equações paramétricas
O que é uma Equações paramétricas ? Denomina-se por equação paramétrica a toda equação quadrática qu…
Calculadora Casio fx-991 Plus
Maquina de calcular Casio fx-991 Plus Temos disponível calculadora cientifica Casio fx-991 Plus, est…
Equações Lineares ou equação do 1º grau
Equação linear ou equação do 1º grau é toda a equação do tipo ax+b=0 onde: a é o coeficiente de x e…
Apostila de Cálculos de limites (Ebook de calculo I)
Apostila de cálculo de limite Você sabia que tem um Ebook de cálculo de limites que pode ajudar você…
Resolução de (Teste I) de Calculo I UNIFEI
1) Calcule caso exista. Se não existir explique o por quê:Primeiro vamos Substituir onde vem x pela …
Exercícios sobre limites e continuidades
No numerador temos uma expressão modular primeiro vamos tirar o módulo. Sabemos que:Como os limites …
Acréscimo de uma função
Conceito de acréscimo(∆y) de uma função f(x) Seja dada a função f(x) cujo o gráfico ê a baixo repres…
Apostila de Cálculos de limites (Ebook de calculo I)
Apostila de cálculo de limite Você sabia que tem um Ebook de cálculo de limites que pode ajudar você…
Aplicação da primeira e segunda derivada extremos e ponto de infecção
Estudo da primeira derivada Seja uma função f(x) continua Assim temos representado os gráficos de um…
Teoria de ácido e base segundo Bronsted-Lowry
Ácido e base segundo Bronsted-Lowry Com as limitações apresentadas na definição de ácido e base segu…
Teoria de ácido e bases de Arrhenius
Ácido segundo Arrhenius Segundo Arrhenius ácido é qualquer substância que reagindo com água sofre io…
Força Relativa de um Ácido e uma Base em solução aquosa
Força Relativa de um Ácido A força relativa de um acido é determinada pela sua tendência de ceder pr…
As bolas do mundial 2022 são recarregadas?
A bola do mundial 2022 tem um sensor de toque e movimento dentro dela, com o objectivo de fornecer i…
Movimento uniformemente variado
O que é movimento uniformemente variado Movimento uniformemente variado é aquele em que a veloc…
Movimento uniforme
Movimento uniforme Movimento uniforme é aquele em que a velocidade instantânea permanece c…

















