Integral de funções com fracções ( com raiz no denominador)

Integral de fracções com raiz no denominador Primeiro tipo

Para integramos essa função vamos transformar a expressão que esta na raiz numa expressão do tipo

Relembrando as formulas de integrais que fracções com raiz no denominador;

Onde para as nossas integrais o “u” vale “x+m” então as soluções das nossas integrai serão;

Resolução de exercícios Integral de funções com fracções com raiz no denominador

Vamos transformar a expressão que esta na raiz numa expressão do tipo (x+m)²+n²

x²+4x+8=x²+2•2x+8= x²+2•2x+2²-2²+8=(x+2)²+4

Transformaremos 4 em 2 ao quadrado e depois iremos usar a nossa forma de integral de uma fracção dentro da raiz e assim temos o resultado da nossa integral.

sabemos que x²-6x-16=x²-2•3x-16= x²-2•3x+3²-3²-16=(x-3)²-25 substituindo x²-6x-16 por (x-3)²-5² na nossa integral temos :

Recorrendo aos mesmos procedimento que fizemos nos exercícios acima

-x²+8x+20=-(x²-8x-20)= -(x²-2•4x+4²-4²-20)=-((x+4)²-36)=-( x+4)²+6²

-( x+4)²+6² podemos escrever como 6²-( x+4)² e nos recordamos das integrais que resultam em arcseno

Iremos escrever a expressão que esta dentro da raiz como x²+10x+25=x²+2•10x+5²=(x+5)²

Simplificaremos o ao quadrado com a raiz e assim teremos integral de 1 sobre x+5 e essa integral resultam em ln |x+5|.

Integral de fracções com raiz no denominador segundo tipo

Nesse tipo de integral precisamos de ter a derivada da expressão que esta dentro da raiz no numerador adicionado a uma constante depois separa a integral em duas integrais e por fim resolver cada uma das integrais.

Separamos a nossa integral em duas integrais

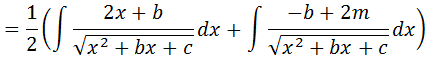
Tirando as contastes que estão dentro da integral para fora da integral temos;

Devemos por fim calcular I₁ e I₂ e assim temos a solução da nossa integral

Vamos seguir os passos que aprendemos anteriormente , Vamos multiplicar o numerador por 2 e multiplicar a nossa integral por (1/2) para tirar o dois que nos multiplicamos no numerador

Como queremos ter a derivada da expressão que esta na raiz no numerador vamos adicionar 4 e subtrair 4

Vamos somar -4 e -6 que resulta em -10

Separando a nossa integral em duas integrais temos;

Vamos calcular cada uma das nossas integrais

Agora vamos calcular a primeira integral, como a derivada da expressão que esta na raiz esta no numerador vamos usar o método de substituição

x²+4x+8=u

(2x+4)dx=du

Vamos agora para integral principal

Substituindo I₁ e I₂ pelas espressoes equivalentes temos

Simplificaremos o 1/2 e 2 e escreveremos (x+2)²+2² como sendo x²+4x+8

A solução do nosso exercício é :

Para resolver essa integral primeiro vamos tirar o 4 para fora da raiz

Evidenciando o 3 no numerador e tirando o 4 para fora de raiz temos;

Vamos multiplicar o numerador por -2 e multiplicar a nossa integral por (-1/2) para que seja uma expressão equivalente.

Para que a derivada da expressão que esta dentro raiz esteja no numerador no numerador temos que ter -2x+8 ja temos o -2x falta o 8 então vamos adicionar 8 e tirar 8 (+8-8)

Somando -8 e 4 temos -4;

Aplicando a propriedade da integral da soma iremos separar a nossa integral em duas integrais

Vamos calcular separadamente dada uma das integrais

Calcularemos a primeira integral (I₁) usando o método de substituição

-x²+8x+20=u

(-2x+8)dx=du

Iremos agora substituir a expressão de I₁ e I₂ na nossa integral principal

Já temos a solução do nosso exercício que é :

Aulas relacionadas

• Calculo integral
• Derivada de arcseno
• Integral de funções que resulta em uma função logaritmo
• Integral de funções exponencial
• Integral de método substituição
• Limites trigonométricos