O que são equações trigonométricas
Equações trigonométricas são equações que uma ou mais expressão trigonométrica.
Relações trigonométricas usadas na resolução de equações trigonométricas.
* sen(x)=cos(x+90°)
* cos (x)=sen(x+90°)
*tan (x)=ctg(x+90°)
*ctg (x)=tan(x+90°)
* sen2(x)+cos2(x)=1
* sen(a+b)=sen(a)cos(b)+ sen(b)cos(a)
* sen(2a)=2sen(a)cos(b)
* cos(a+b)=cos(a)cos(b)- sen(a)sen(b)
* cos(2a)=cos2(a)- sen2(a)
Equações trigonométricas do tipo com seno
sen(x)=sen(a)
Para resolver essa equação trigonométrica temos que ter em conta que as Equações trigonométricas são periódicas e o período da função seno que é 2πk com (k é um numero inteiro), e que a equação tem solução no primeiro quadrante também terá solução no segundo quadrante (vice versa), e se a equação tem solução no terceiro quadrante também tem solução no terceiro quadrante (vice versa).
Solução de equação trigonométrica do tipo seno
sen(x)=sen(a)
x=a+2 πk ou x=(π-a)+ 2 πk
Equações trigonométricas do tipo com cosseno
cos(x)=cos(a)
Para resolver essa equação trigonométrica do tipo cosseno temos que ter em conta o período que é 2 πk, e recordar que a função cosseno é uma função par o que quer dizer que cos(a)= cos(-a).
Solução de equação trigonométrica do tipo cosseno
cos(x)=cos(a)
x=a+2 πk ou x=-a+ 2 πk
Equações trigonométricas exercícios
Resolve as seguintes equações trigonométricas
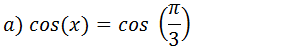
Resolução
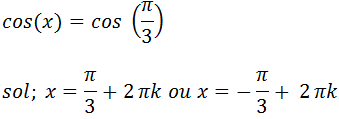
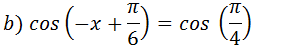
Resolução
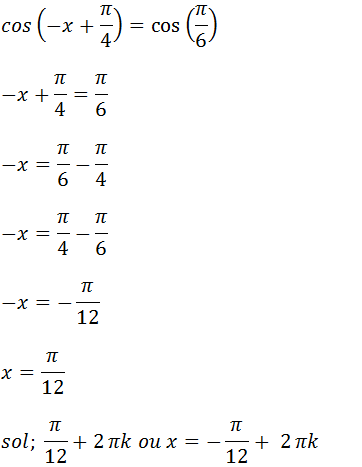
c) 2 cos(2x-π) = 1
Resolução
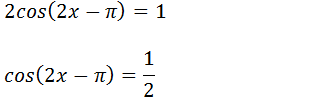
vamos temos que procurar um ângulo cujo o seu cosseno seja 1/2 e esses ângulo é 60˚ que corresponde a π/3. (veja tabela de ângulos especiais )
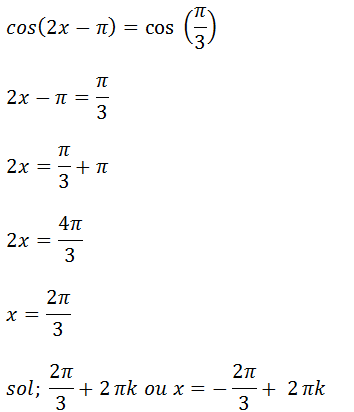
Exercícios de equacoes trigonométrica envolvendo seno
resolucao
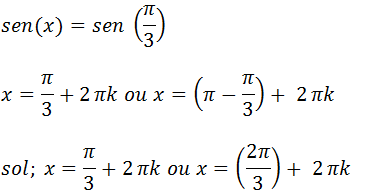
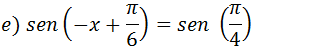
Resolução
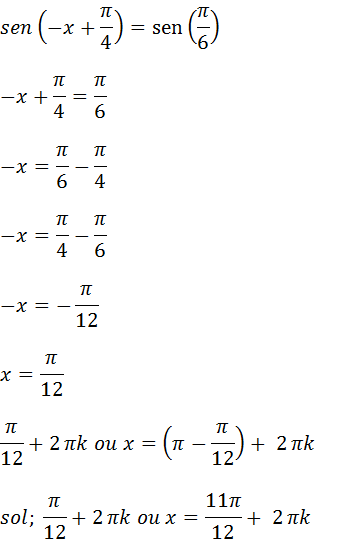
f) 2 sen(2x-π) = 1
Resolução
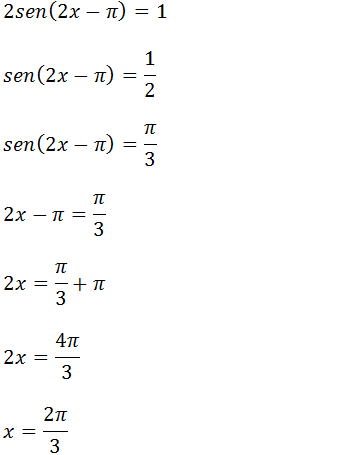
Agora vamos dar a solução geral
Resolução de equações trigonométricas no primeiro no quadrante
Calcule o valor de x tendo em conta que x e um ângulo do primeiro quadrante.
resol
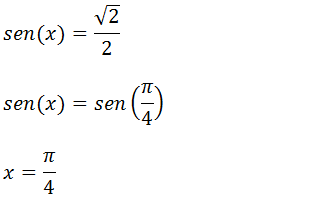
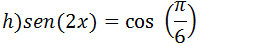
Resolução
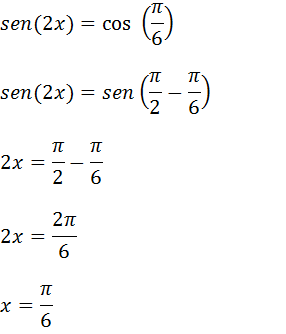
i)4sen2 (x)-4sen(x)=-1
Resolução
4sen2 (x)-4sen(x)=-1
4sen2 (x)-4sen(x)+1=0
Seja; sen(x)=t
4t2-4t+1=0
estamos diante de uma equação quadrática
i)2cos2(x)+4=9cos(x)
Resolução
2cos2(x)+4=9cos(x)
2cos2(x)-9cos(x)+4=0
Seja; cos(x)=t
2t2-9t+4=0
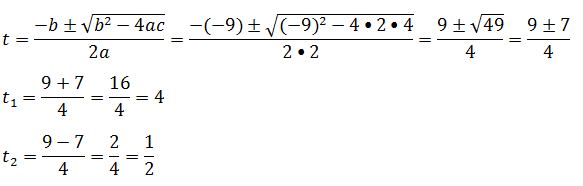
Como cos(x) esta entre 1 e -1 então t eu vamos considerar é apenas 1/4
Entre os ângulos especiais nenhum ângulo tem cosseno igual a ¼ então por isso tivemos que recorrer a função inversa.
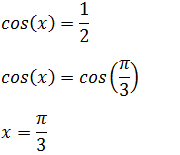
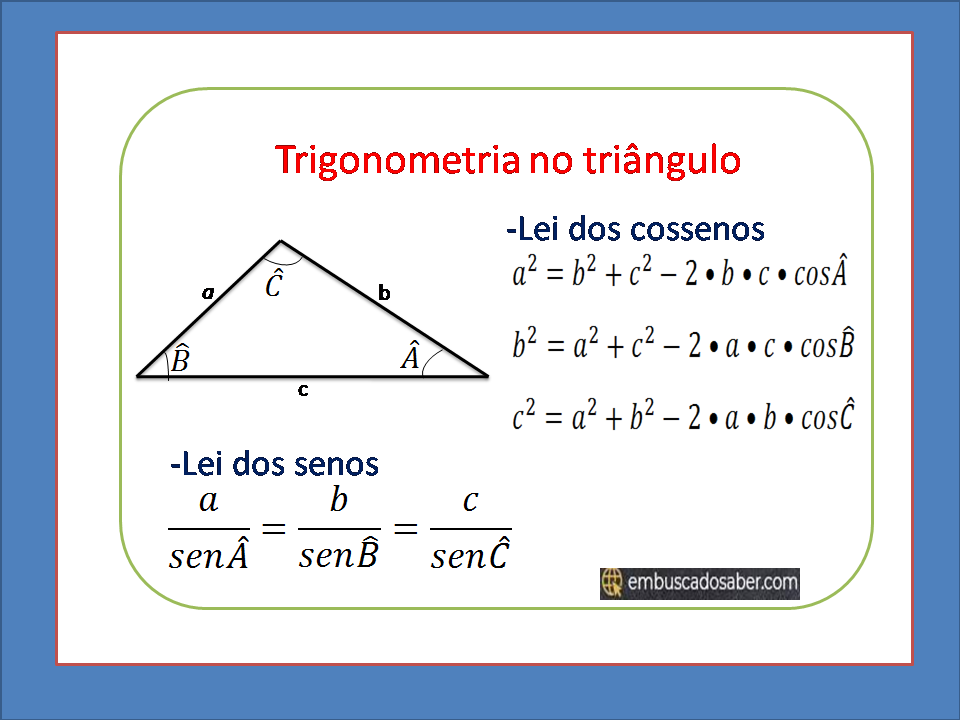
lei dos cossenos e lei dos senos
Lei dos cossenos Seja da um triângulo A lei dos cossenos relaciona os lados desse triângulo e os ângulos de tal modo que com dois lados e o ângulo oposto ao lado desejado seja possível determinar a me…
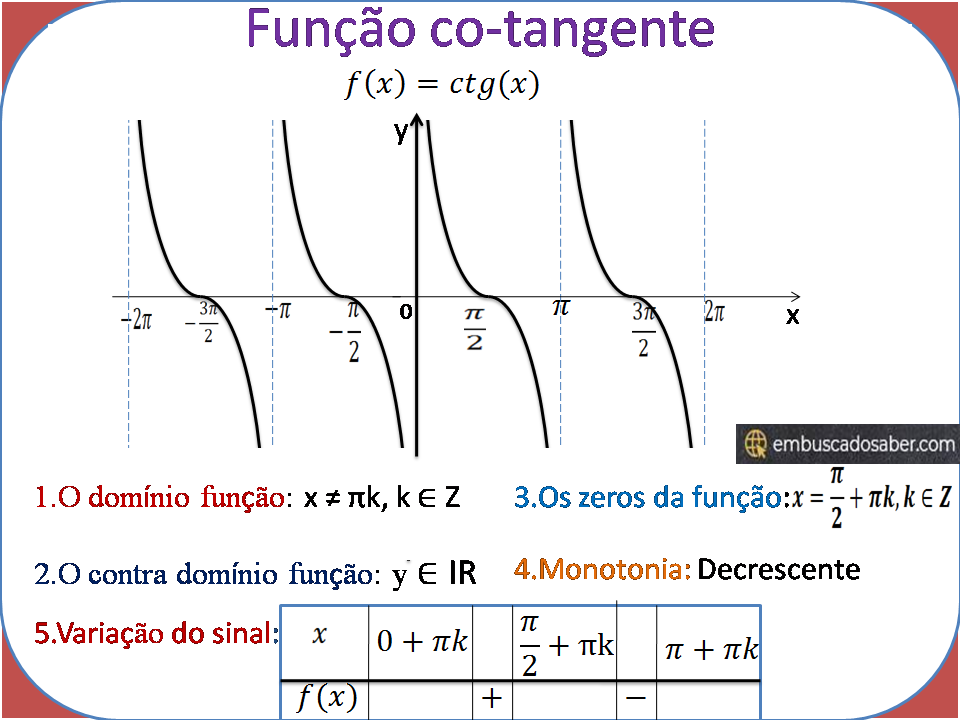
Funções trigonométricas função co-tangente
Funções trigonométricas função co-tangente y=ctg(x) A função co-tangente f(x)= ctg(x) é definida como a razão entre a função g(x)=cos(x) e a função h(x)=sen(x) . Com isso podemos claramente notar que …
Funções trigonométricas função tangente
Função tangente A função tangente f(x)=tan(x) é definida como a razão entre a função g(x)=sen(x) e a função h(x)=cos(x) . Com isso podemos claramente notar que função tangente tem zeros sempre que sen…
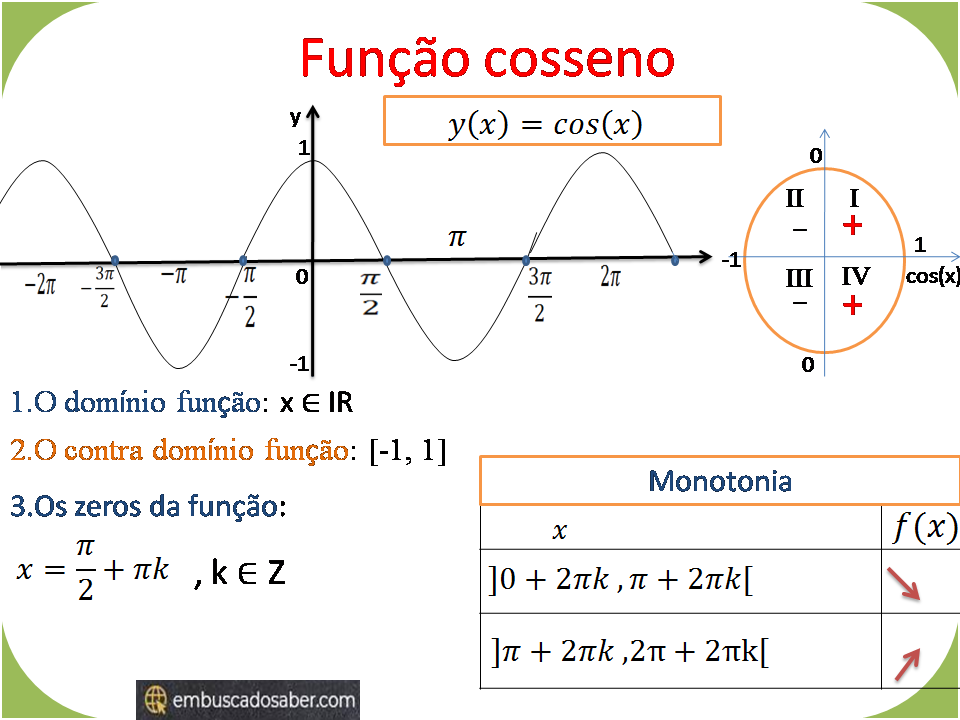
Funções trigonométricas função cosseno y=cos(x)
Função cosseno y=cos(x) Representação gráfica da função y=cos(x) Para representar o gráfico da função seno iremos construir uma tabela onde atribuiremos valores e x e encontrares com base nesses valor…
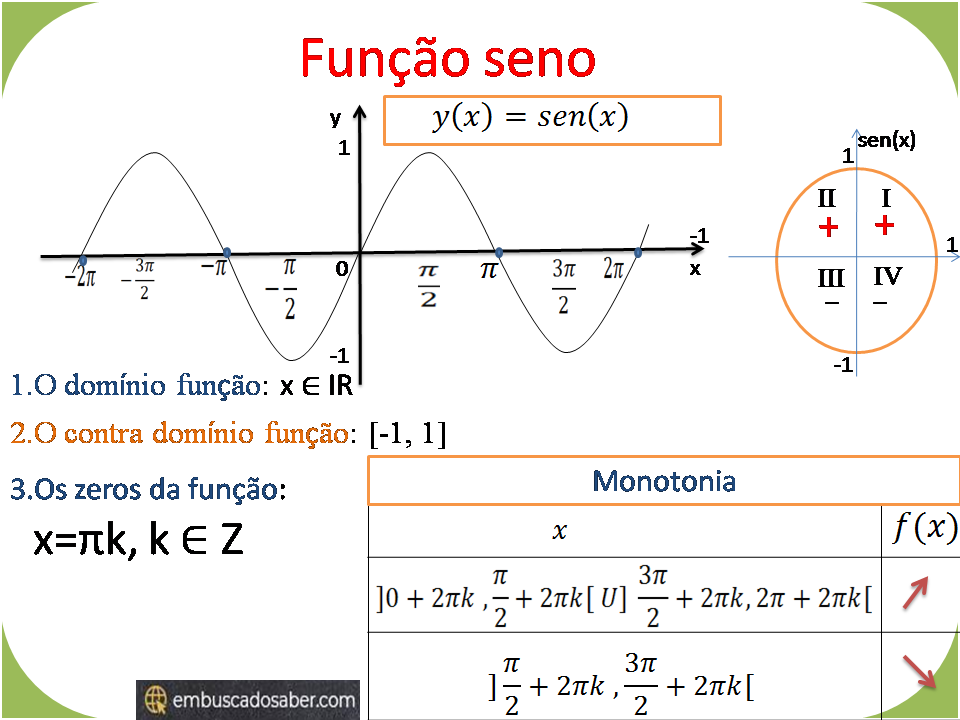
Funções trigonométricas função seno y=sen(x)
Funções trigonométricas As principais funções trigonométricas são função seno, função cosseno, função tangente e a função co-tangente. Nesse capítulo iremos aprender a como representar graficamente es…
Apostila de Cálculos de limites (Ebook de calculo I)
Apostila de cálculo de limite Você sabia que tem um Ebook de cálculo de limites que pode ajudar você a ter um bom desempenho académico na disciplina de cálculo I. Uma apostila feito para você aprender…
Diagrama de Venn
O que é diagrama de Venn O diagrama de Venn é uma forma Matemática usada para representar um conjunto de dados. Como representar os dados no diagrama de Venn Como primeira dica para representar os dad…
Lógica Matemática ( operações lógicas e proposições)
Lógica Matemática A lógica matemática estuda o raciocínio matemático Valor lógico Os valores lógicos são verdadeiro e falso (V e F) O que é uma preposição? Uma preposição é uma expressão lógica que po…
Tipos de conjuntos (Teoria de conjuntos)
O que é um conjunto ? Conjunto é um agrupamento que pode ser de seres, números objectos etc, com as mesmas características. Elemento de um conjunto Elemento de um conjunto é cada objecto do conjunto S…
Operações entre conjuntos (teoria de conjuntos)
Operações entre conjuntos As principais operações entre conjuntos são; * União (U) * Intercessão (∩) * Complementar de um conjunto * Diferença (A/B) * Diferença simétrica ∆ União de conjuntos (AUB) A …
lei dos cossenos e lei dos senos
Lei dos cossenos Seja da um triângulo A lei dos cossenos relaciona os lados desse triângulo e os ângulos de tal modo que com dois lados e o ângulo oposto ao lado desejado seja possível determinar a me…
Equações trigonométricas
O que são equações trigonométricas Equações trigonométricas são equações que uma ou mais expressão trigonométrica. Relações trigonométricas usadas na resolução de equações trigonométricas. * sen(x)=co…
Funções trigonométricas função co-tangente
Funções trigonométricas função co-tangente y=ctg(x) A função co-tangente f(x)= ctg(x) é definida como a razão entre a função g(x)=cos(x) e a função h(x)=sen(x) . Com isso podemos claramente notar que …
Funções trigonométricas função tangente
Função tangente A função tangente f(x)=tan(x) é definida como a razão entre a função g(x)=sen(x) e a função h(x)=cos(x) . Com isso podemos claramente notar que função tangente tem zeros sempre que sen…
Funções trigonométricas função cosseno y=cos(x)
Função cosseno y=cos(x) Representação gráfica da função y=cos(x) Para representar o gráfico da função seno iremos construir uma tabela onde atribuiremos valores e x e encontrares com base nesses valor…
Funções trigonométricas função seno y=sen(x)
Funções trigonométricas As principais funções trigonométricas são função seno, função cosseno, função tangente e a função co-tangente. Nesse capítulo iremos aprender a como representar graficamente es…
Funções logarítmicas (Representação gráfica e estudo completo)
O que são funções logaritmicas? O que são funções logaritmicas? Funções logarítmicas são funções em que a variável esta no logaritmano, não basta só saber o concito de funções logarítmicas e necessári…