Funções trigonométricas função co-tangente y=ctg(x)
A função co-tangente f(x)= ctg(x) é definida como a razão entre a função g(x)=cos(x) e a função h(x)=sen(x) .
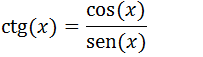
Com isso podemos claramente notar que função tangente tem zeros sempre que cos(x)=0 e não esta definida para sen(x) ≠ 0.
Domino da função ctg(x)
Como a função tangente é a razão entre duas função e conforme sabemos não existe divisão por zero então como já dissemos sen(x) ≠ 0
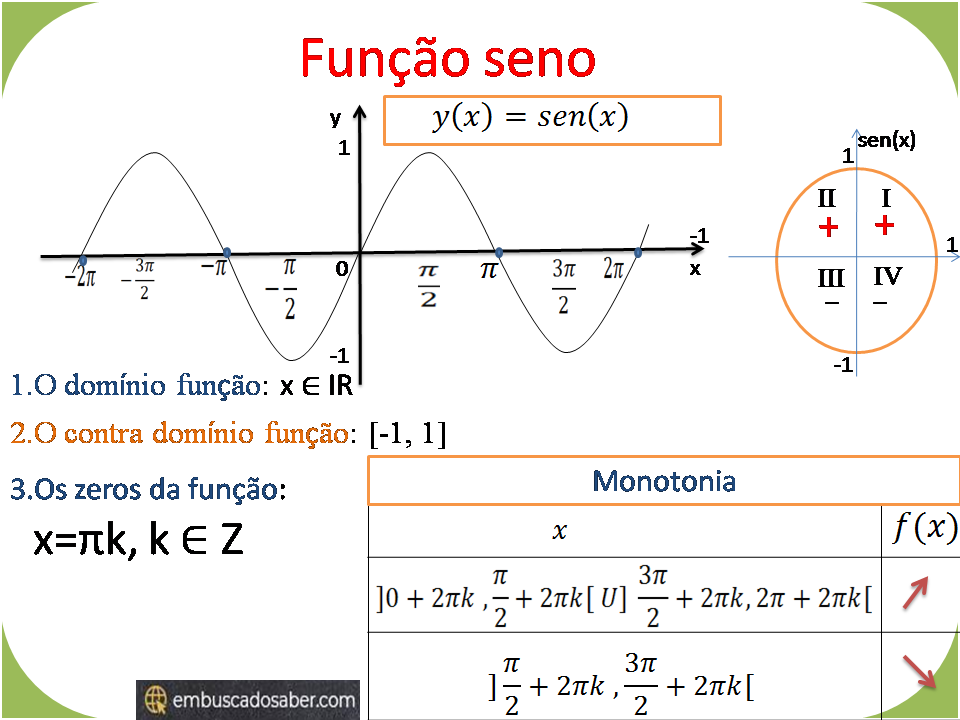
Quando estudamos a função trigonométrica k(x)=sen(x) vimos que os zeros são;
x = πk, k ∈ Z
Então podemos de dizer que para a função f(x)= ctg(x)
Df; x ≠ πk, k ∈ Z
Zeros da função para função f(x)=ctg(x)
Sabemos que ctg(x)=cos(x)/sen(x) então a função ctg(x) tem zeros sempre que cos(x)=0 lembrar que quando estudamos a função trigonométrica l(x)=cos(x) vimos que essa função tem zeros em x=π/2 + πk, k∈Z então podemos dizer que ;
Para a função f(x)=ctg(x) tem zeros em;

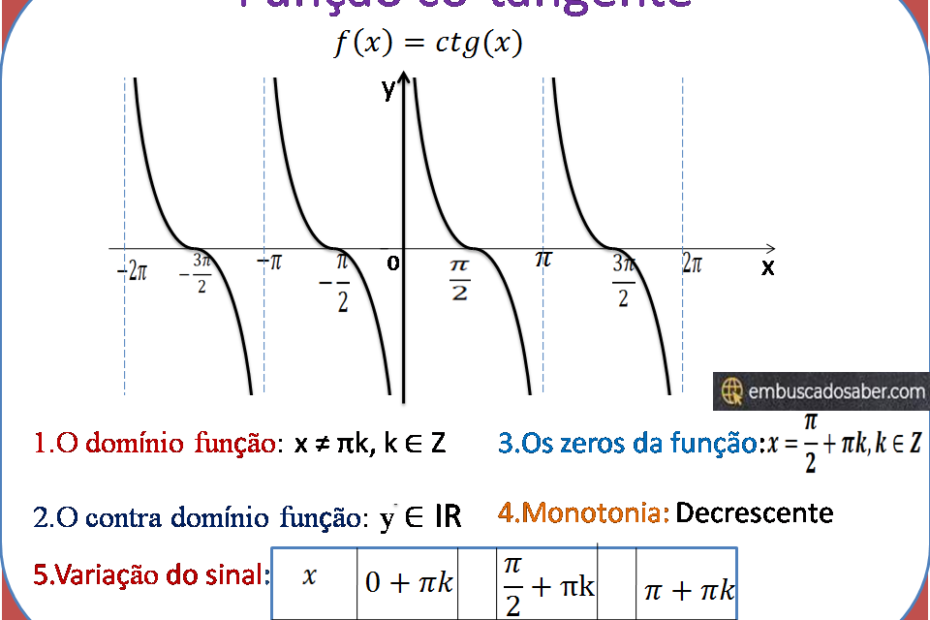
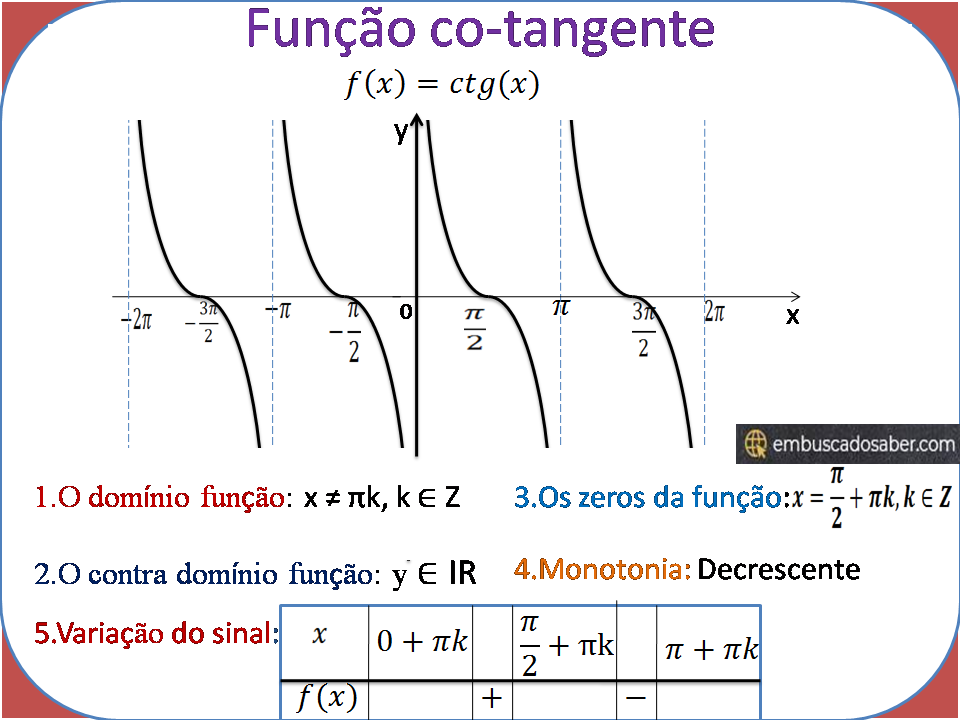
Representação gráfica da função y=ctg (x)
Para representar o gráfico da função tangente iremos construir uma tabela onde atribuiremos valores e x e encontrares com base nesses valores o valore de y.
| x | y=ctg(x) |
| 0 | – |
| π/2 | 0 |
| π | – |
| 3π/2 | 0 |
| 2π | – |

Estudo completo da função trigonométrica y=ctg(x)
Dominio: x ∈ R
Df; x ≠ πk, k ∈ Z
Contra domínio: y ∈ R
Paridade: Impar
Zeros:
Monotonia
A função co-tangente conforme podemos ver no gráfico é uma função decrescente.
Variação do sinal
| x | 0+πk | π/2+πk | π+πk | ||
| y=ctg(x) | + | – |
Veja outras funções trigonométricas
*Função trigonométrica tangente y=tan(x)
*Função trigonométrica seno y=sen(x)
*Função trigonométrica cosseno y=cos(x)
*Trigonometria no triângulo rectângulo
*Derivada de função trigonométrica co-tangente
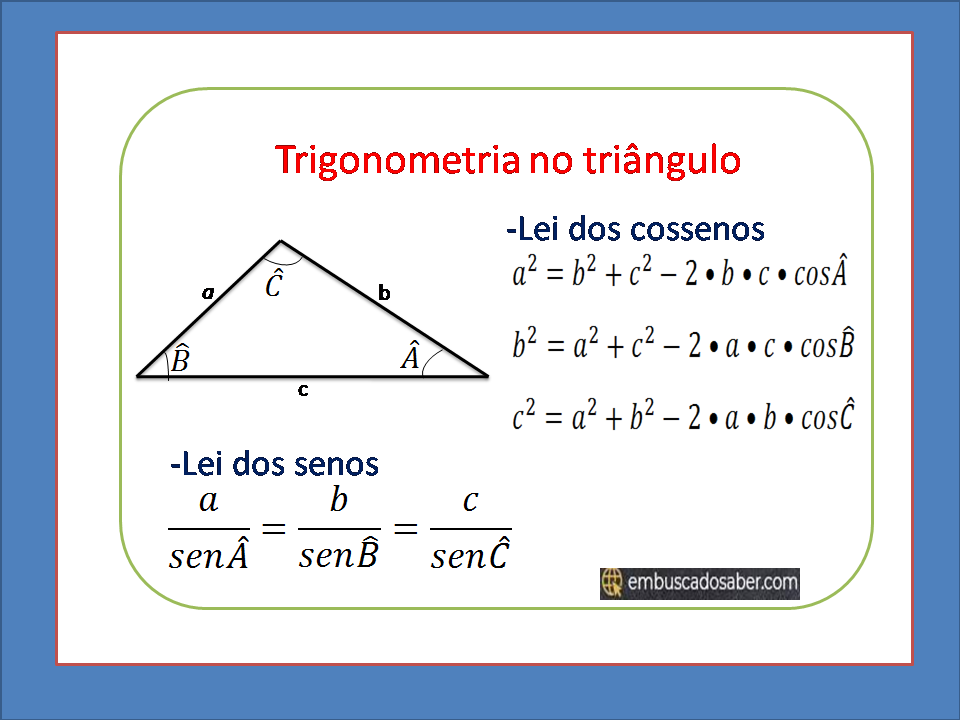
lei dos cossenos e lei dos senos
Lei dos cossenos Seja da um triângulo A lei dos cossenos relaciona os lados desse triângulo e os âng…
Funções trigonométricas função co-tangente
Funções trigonométricas função co-tangente y=ctg(x) A função co-tangente f(x)= ctg(x) é definida com…
Funções trigonométricas função tangente
Função tangente A função tangente f(x)=tan(x) é definida como a razão entre a função g(x)=sen(x) e a…
Funções trigonométricas função cosseno y=cos(x)
Função cosseno y=cos(x) Representação gráfica da função y=cos(x) Para representar o gráfico da funçã…
Funções trigonométricas função seno y=sen(x)
Funções trigonométricas As principais funções trigonométricas são função seno, função cosseno, funçã…
Acréscimo de uma função
Conceito de acréscimo(∆y) de uma função f(x) Seja dada a função f(x) cujo o gráfico ê a baixo repres…
Apostila de Cálculos de limites (Ebook de calculo I)
Apostila de cálculo de limite Você sabia que tem um Ebook de cálculo de limites que pode ajudar você…
Aplicação da primeira e segunda derivada extremos e ponto de infecção
Estudo da primeira derivada Seja uma função f(x) continua Assim temos representado os gráficos de um…
Calculo aproximado usando derivada
Definição derivada Para percebemos como usar as derivadas para fazer o cálculo aproximado vamos usar…
Resolução de (Teste I) de Calculo I UNIFEI
1) Calcule caso exista. Se não existir explique o por quê:Primeiro vamos Substituir onde vem x pela …
Derivada de uma função exponencial
Para acharmos a derivada de uma função exponencial vamos o usar a definição de deriva…
Derivada de uma função usando definição
Definição de derivadas Chamamos de derivada da função f(x) no ponto qualquer a inclinação …
Derivada de uma função
Depois de termos aprendendo o conceito de derivada agora é a hora de aprendemos a cal…
Derivada de funções implícitas
Antes de aprendermos a derivar uma função implícita é necessário saber o que é uma fu…
Derivada de funções paramétricas
Derivada de funções paramétricas Seja y=f(t) e x=g(t) nesse caso podemos afirmar que…
Cálculo de limite usando L’Hospital (Cálculo de limite usando derivadas)
Regra L’Hospital para o calculo de limite A regra de L’Hospital consiste em utilizar o conhecimento …
Cálculo de derivada usando logaritmização
Calcular derivada usando logaritmização ajuda-nos a resolver derivadas que parecem difícil de c…